线性结构与非线性结构
线性结构 Linear Structure
- 线性结构是最常用的数据类型,数据元素之间存在一一对应的关系
- 可以存储为顺序存储(分配内存时,地址是连续的,如数组)和链式存储(地址不一定连续,节点依靠指针,如链表)
- 常见线性结构:数组、队列、链表、栈
非线性结构 Nonlinear Narrative
- 非一对一
- 包括:二维数组、多为数组、广域表、树结构、图结构
稀疏数组 Sparse Matrix
需求与应用
当一个数组大部分是0或同一个值时,可以使用稀疏数组来存储,处理方法:
- 第一行记录有几行几列,有多少不同的值
- 把具有不同值的行列以及对应的值存在一个小规模数组中,缩小程序
如使用二维数组存储一个棋盘(围棋、五子棋等)或地图等,数组上很多位置都是0,记录了很多没有意义的数,可以使用稀疏数组。
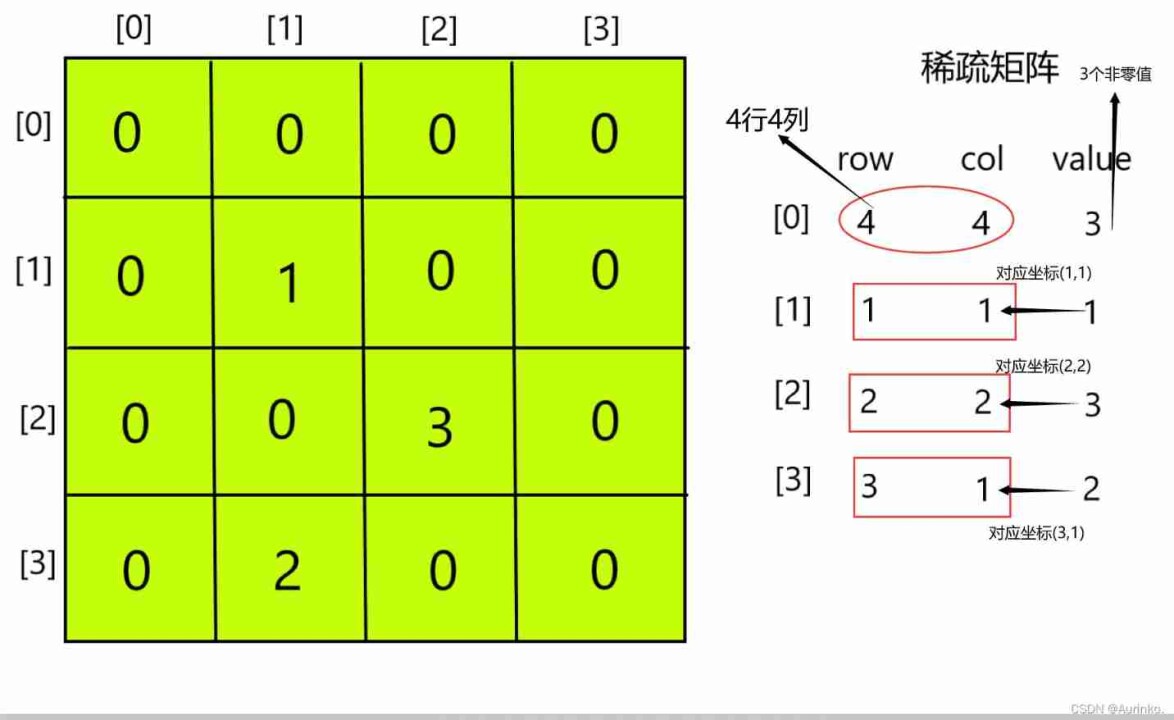
如上图所示,普通数组需要存储16个值,而稀疏数组只存储了12个值。
程序实现
二维数组 to 稀疏数组
- 遍历原始的二维数组,得到有效数据的个数sum
- 根据sum创建稀疏数组,sparseMatrix int[sum+1][3], 行的数量取决于有效数据的数量
- 将数据存储到稀疏数组
稀疏数组 to 二维数组
- 根据第0行的数据创建原始数组 originMatrix int [4][4](如上图的4*4)
- 读取稀疏数组后几行的数据并赋值给二维数组
代码
public class sparseMatrix {
public static void main(String[] args) {
// create a int[4][4] matrix and give the number as the picture above
int[][] matrix = new int[4][4];
matrix[1][1] = 1;
matrix[2][2] = 3;
matrix[3][1] = 2;
// print the matrix
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
// trans the matrix to sparse matrix
// iterate over the two-dimensional matrix and get the "sum"
int sum = 0;
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if (matrix[i][j] != 0) {
sum++;
}
}
}
System.out.println("the sum of the matrix is " + sum);
// create a sparse matrix
int[][] sparseMatrix = new int[sum + 1][3];
sparseMatrix[0][0] = matrix.length;
sparseMatrix[0][1] = matrix[0].length;
sparseMatrix[0][2] = sum;
// iterate over the two-dimensional matrix and get the numbers != 0
int count = 0;
for (int i = 0; i < sparseMatrix.length; i++) {
for (int j = 0; j < sparseMatrix[i].length; j++) {
if (matrix[i][j] != 0) {
count++; // count the number of the numbers != 0
sparseMatrix[count][0] = i; // fist column = i
sparseMatrix[count][1] = j; // secod column = j
sparseMatrix[count][2] = matrix[i][j]; // third column = matrix[i][j]
}
}
}
// print the sparse matrix
for (int i = 0; i < sparseMatrix.length; i++) {
for (int j = 0; j < sparseMatrix[i].length; j++) {
System.out.print(sparseMatrix[i][j] + " ");
}
System.out.println();
}
/*
* trans to sparse matrix finished
* now let's trans the sparse to origin matrix
*/
// read the first line of the sparse matrix
int[][] originMatrix = new int[sparseMatrix[0][0]][sparseMatrix[0][1]];
for (int i = 1; i < sparseMatrix.length; i++) {
originMatrix[sparseMatrix[i][0]][sparseMatrix[i][1]] = sparseMatrix[i][2];
// if can not understand, please refer to the picture above
}
// print the origin matrix
for (int i = 0; i < originMatrix.length; i++) {
for (int j = 0; j < originMatrix[i].length; j++) {
System.out.print(originMatrix[i][j] + " ");
}
System.out.println();
}
}
}输出
0 0 0 0
0 1 0 0
0 0 3 0
0 2 0 0
the sum of the matrix is 3
4 4 3
1 1 1
2 2 3
3 1 2 队列 Queue
需求与应用
- 队列是一个有序列表,可以用数组或链表实现
- 先入先出,即先进入的数据先取出(与栈相反)
例如银行、医院的排队系统、羽毛球筒球的存放
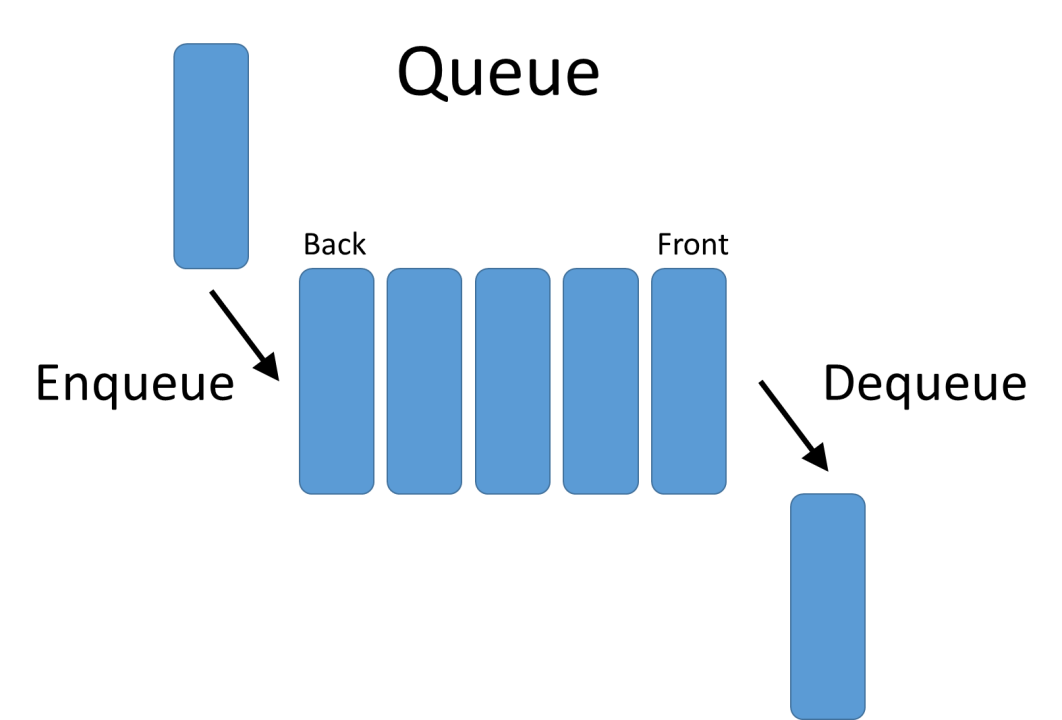
先使用数组情况来说明,maxSize 用于存储数组的容量(即index+1),输入和输出分别由队列的后、前端来处理。因此,需要两个变量(指针) front 和 rear 来记录队列前、后端的 index 。 front 随数据输出而而+1,rear 则根据输入+1。
front初始指向最前面的元素的index-1,rare指向最后一个元素。初始化时rare==front==-1
程序实现
判断队列是否为满 isFull
判断rare指针是否为rare == maxSize-1,即数组的最大index
判断队列是否为空 isEmpty
即判断是否处于状态rare==front
入队 Enqueue
- 判断队列是否为满
- 将尾部指针后移rare+=1
- 加入数据queue[rare]=data
出队 Dequeue
- 判断队列是否为空
- front指针加1
- 输出queue[front](front指向的是前一个位置)
本程序中对于取出后的数字不清零,即数组对应位置上的元素不便,只是front变化
代码
import java.util.Scanner;
public class arrayQueue {
public static void main(String[] args) {
ArrayQueue queue = new ArrayQueue(5);
char key = ' ';
Scanner scanner = new Scanner(System.in);
while (true) {
System.out.println("s(show): show queue");// give some suggestions to user
System.out.println("e(exit): exit");
System.out.println("a(add): add element");
System.out.println("g(get): get element");
key = scanner.next().charAt(0);//get a char
switch (key) { // a switch statement to handle the different cases
case 's':
queue.showQueue();
break;
case 'e':
System.exit(0);
break;
case 'a':
System.out.println("input a element:");
queue.enqueue(scanner.nextInt());
break;
case 'g':
System.out.println("get element:" + queue.dequeue());
break;
default:
System.out.println("wrong input!");
break;
}
}
}
}
class ArrayQueue {
private int maxSize, front, rare;// front is the index of the first element
// rare is the index of the last element
private int[] arr;// store the data in the array queue
// constructor
public ArrayQueue(int maxSize) {
this.maxSize = maxSize;
arr = new int[maxSize];
front = -1;// initialize the front to -1,point to the head-1 of the queue
rare = -1; // initialize the rare to -1,point to the tail of the queue
}
// isFull
public boolean isFull() {
return (rare == maxSize - 1);
}
// isEmpty
public boolean isEmpty() {
return (front == rare);
}
// enqueue method
public void enqueue(int data) {
if (isFull()) {
System.out.println("The queue is full");
return;
}
if (isEmpty()) {
front = 0;
}
rare++;
arr[rare] = data;
}
// dequeue method
public int dequeue() {
if (isEmpty()) {
System.out.println("The queue is empty");
return -1;
}
front++;
return arr[front];
}
// print the queue
public void showQueue() {
if (isEmpty()) {
System.out.println("The queue is empty");
return;
}
for (int i = front + 1; i <= rare; i++) {
System.out.println(arr[i] + " ");
}
}
}输出与思考
运行该程序即可实现队列的输入输出的模拟,程序中的队列有4个元素(预留了一个空间),但本程序中存在问题:该队列(数组)只能使用一次,当多次使用get数据后,front==rare根据判断条件可知队列为空。
环形队列
为了实现复用和优化,需要转化为环形队列。
环形队列在内存中并不是存储为圆形,只是使用了取模(余数)的方法模拟,让数组成为环形,即两个指针可以达到最大index后,还可以回到index==0的位置,从而实现对一个数组的复用。与此同时需要注意队列为满的条件,防止溢出(数组越界)。
这里借用两张 SCALER Topics 的图片来说明
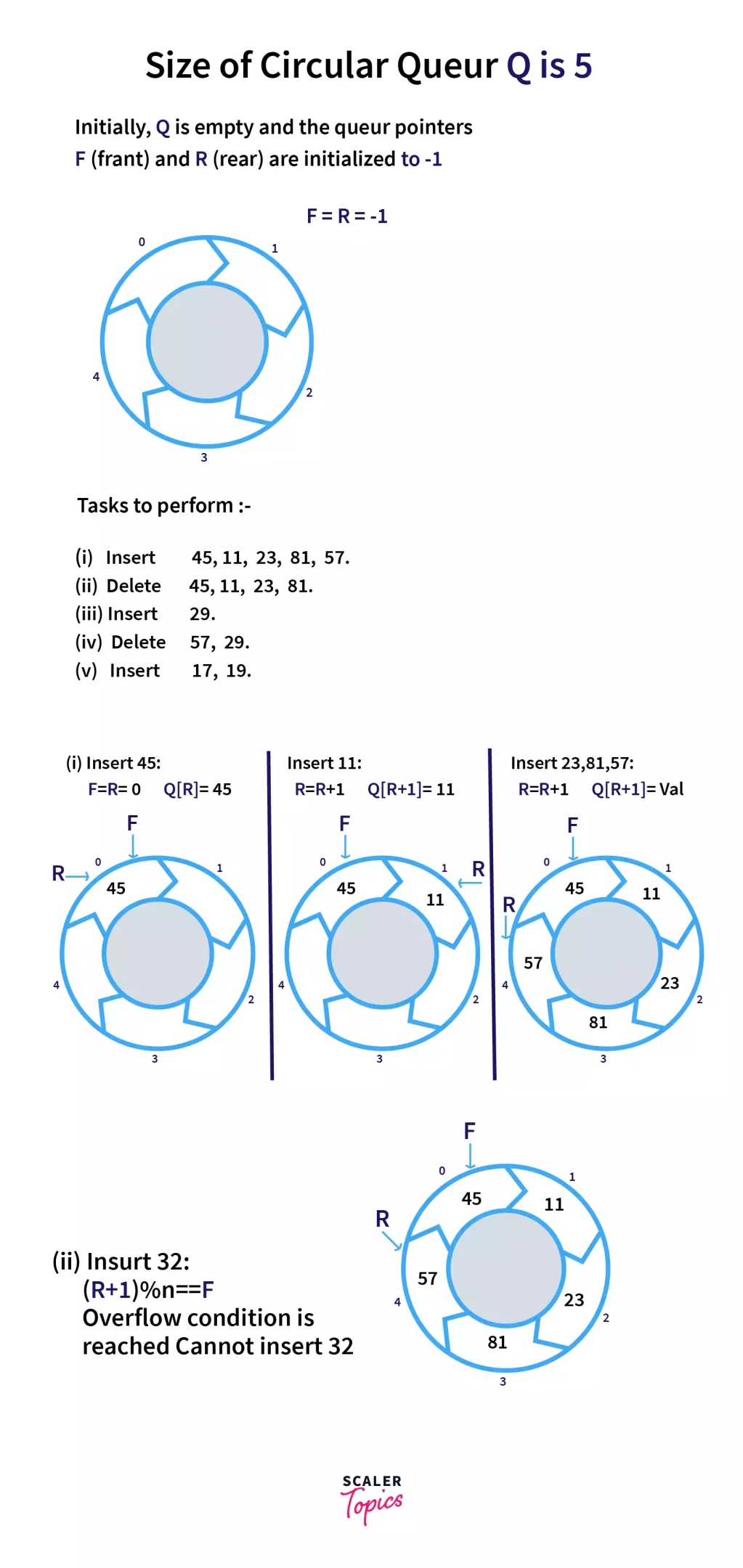
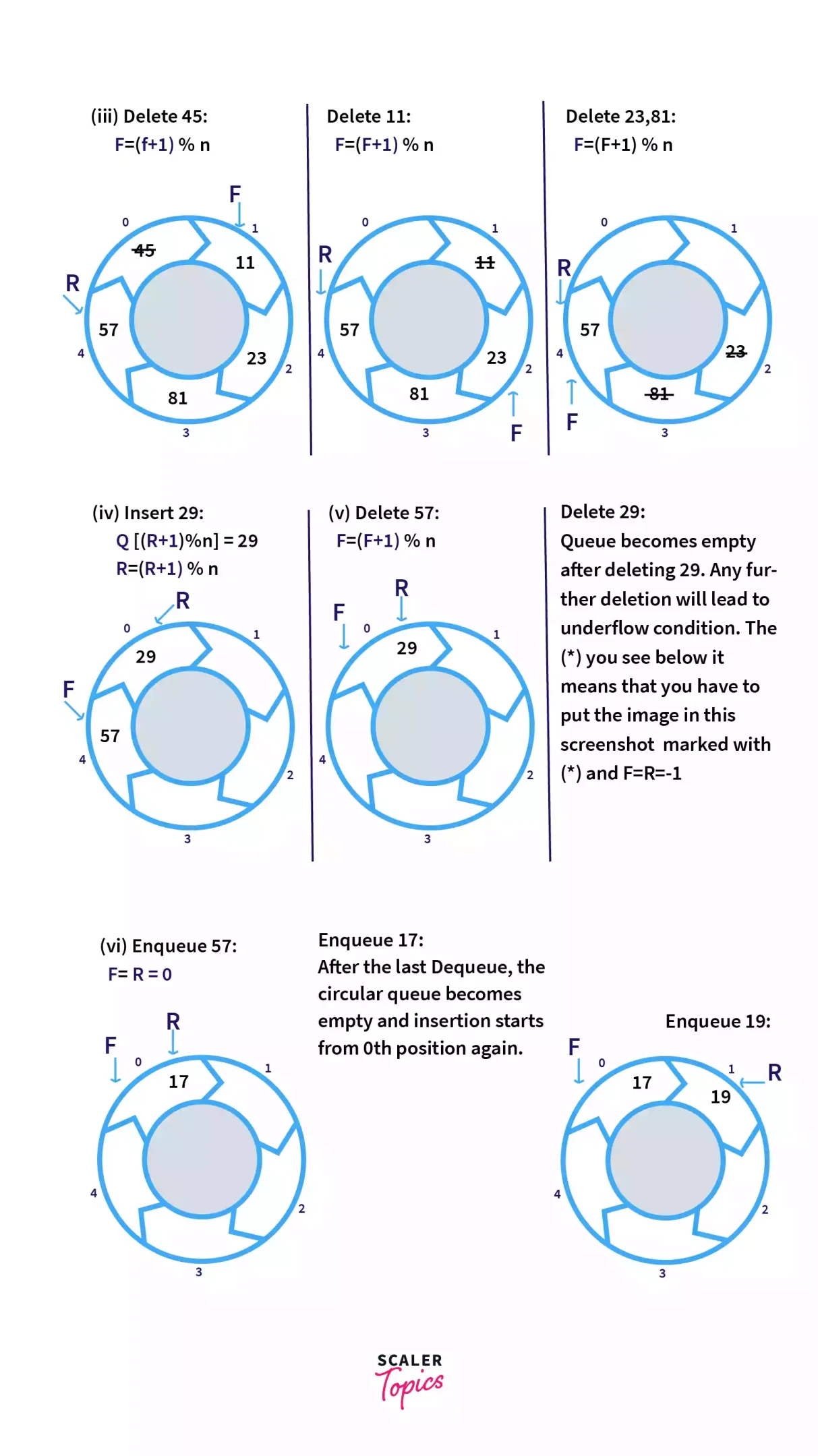
程序实现
- 将 front 指向队列的第一个元素,front 的初始值为-1
- 将 rare 指向队列的最后一个元素,rare 的初始值为-1
- 当队列满时,(rare +1)%maxSize==front
- 当队列只有最后一个元素时,rare == front || front == rare == -1
- 队列中有效数据的个数, rare -front+1
环形队列有多个模拟算法,上述实现方法只是其中一种,分局上述内容,修改上个程序即可实现环形队列
判断队列是否为满 isFull
判断rare指针是否为((rare +1)%maxSize==front)
判断队列是否为空 isEmpty
即判断是否处于状态 (Front == -1 && Rear == -1)
入队 Enqueue
- 判断队列是否为满
- 判断是否是刚初始化的数组,并设置 rare 指针If (isEmpty()) {Front = Rear = 0} else {Rear = (Rear + 1) % N}
- 加入数据queue[rare]=data
出队 Dequeue
- 判断队列是否为空
- 输出queue[front]
- 判断是否是最后一个元素,移动front指针即if (front == rare) {front = rear = -1} else {front =( Front + 1) % N}
以上述方法写出的程序不是完整的环形,但同样模拟出来环形队列,可以尝试修改算法。
单链表 Single Linked List
链表是有序的列表,以节点的方式来存储,每个节点由 data 域、next 域构成,头节点指向第一个地址,第一个地址的next域指向第二个地址,data域存放数据。链表的每个节点不一定是连续存储的。
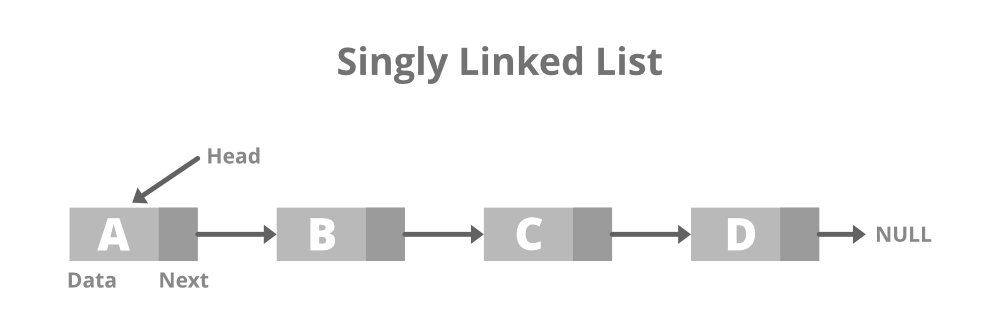
链表包括带头节点的链表和不带头节点的链表,根据需求来决定。链表需要实现的功能是:增、删、改、查。
IMPORTANT:头节点不存放具体的数据,头节点并不是一个完整的节点,而是一个引用变量“指针”,作用就是指向单链表的开头,最后一个节点的 next 域的值为 Null.
思考:head.next相当于第一个实际节点的next域。
同样的,一个数组也能存储这些信息,链表因为next域的存在需要消耗更多的内存,但是若在上图的中的A和B之间插入一个新元素,或者A之前插入一个元素,如果使用数组则会影响到后面所有的数据,甚至整个数组,使用链表则仅仅影响个别元素。
注:JAVA 编写的 linked list 需要使用到方法中的引用变量,可参考:Reference Variable in Java
链表操作的实现方法
创建链表
- 创建一个类(函数)
- 添加基础的属性,即 Data域
- 添加一个引用变量(指针)
- 一个构造器(data域变量赋值)
// Class for Single Linked List
public class SLL {
Node head; // head of list
/* Single Linked list Node*/
class Node {
int data;
Node next;
// Constructor to create a new node
// next is by default initialized as null
Node(int d) { data = d; }
}
}遍历(显示)链表
- 借助一个引用变量(指针),将其指向 head
- 当指向节点的 next 域不为 null 时进行遍历
public void display(Node head){
Node temp = head;
while(temp != null){
System.out.println(temp.data);
temp = temp.next;
}
}添加到链表头部
- 创建一个新的节点
- 判断链表是否为空,即 head == null
- 如果为空,将头节点指向新节点,将新节点的next域设为null(默认就是null)
- 如果非空,将新节点的 next 域指向头节点,将头节点指向新节点
注意:head节点所存的是链表中第一个节点的地址,head没有data域,不是一个真正的节点,将新节点的next域设为头节点,就相当于将新节点的 next 域置为原链表中第一个节点的地址。
public void insertAtStart(Node newNode) {
if (head == null) {
head = newNode;
} else {
newNode.next = head;
head = newNode;
}
}添加到链表尾部
- 从头开始遍历节点直到结束(node.next == Null)
- 将尾部节点指向新节点
- 将新节点的next域修改为 Null
public void insertAtEnd(Node newNode){
Node temp = head;
while(temp.next != null){
temp = temp.next;
}
temp.next = newNode;
newNode.next = null;
}添加到链表中间
- 遍历,直到发现需要插入的位置
- 将新节点指向下一节点
- 将原先的节点指向新节点
public void insertAfterTargetNode(Node newNode, Node head, int target){
Node temp = head;
while(temp.data != target){
temp = temp.next;
}
newNode.next = temp.next;
temp.next = newNode;
}删除节点
以删除中间节点为例,删除头节点或尾节点的方法类似
- 使用一个辅助节点和一个引用变量(指针)
- 开始遍历,直到找到要删除的节点(数据或index等内容匹配)
- 修改节点的 next 域,指向后两个节点
- 如果删除的是head,则使用 head=head.next
void deleteAfterTarget(Node head, int target){
Node temp = head;
while(temp.data != target){
temp = temp.next;
}
temp.next= temp.next.next;
}上述代码中的head、tail等变量可以换为全局变量。
思考与练习
链表的反转:将一个链表倒序排布并输出链表内的信息
对于链表的反转可以利用在链表开头插入元素的方法解决(即头插、双指针)。创建一个新链表用于存储反转后的链表,每向后查看一个节点,将遍历到的节点放在新链表的头部(需要修改节点信息)。
链表倒序输出
可以先反转链表,然后输出,占用大量的空间,会改变原来的链表。可以将链表压住栈中,利用栈的特性来进行倒序输出
双向链表 Double Linked List
单链表只能向一个方向查找,删除一个节点时,要依靠一个辅助节点,不能自我删除。
双向链表拥有指向下一个节点的 next 域和指向前一个节点的 pre 域。

双链表操作的实现方法
遍历的方式和单链表一样,可以向前查找,也可以向后查找。遍历、修改方法和单链表基本相同。
创建双链表
相比较单链表,仅仅增加了一个 prev 引用变量。
// Class for Doubly Linked List
public class DLL {
Node head; // head of list
/* Doubly Linked list Node*/
class Node {
int data;
Node prev;
Node next;
// Constructor to create a new node
// next and prev is by default initialized as null
Node(int d) { data = d; }
}
}添加到链表尾部
- 遍历,找到最后一个节点
- temp.next = newNode
- newNode.pre = temp
删除节点
- 找到要删除的节点
- deleteNode.pre.next = temp.next
- deleteNode.next.pre = temp.pre
void deleteNode(Node del)
{
// Base case
if (head == null || del == null) {
return;
}
// If node to be deleted is head node
if (head == del) {
head = del.next;
}
// Change next only if node to be deleted
// is NOT the last node
if (del.next != null) {
del.next.prev = del.prev;
}
// Change prev only if node to be deleted
// is NOT the first node
if (del.prev != null) {
del.prev.next = del.next;
}
// Finally, free the memory occupied by del
return;
}其它类型的链表
环形链表(约瑟夫环)
约瑟夫问题:设编号1,2,3——n的人坐一圈,约定编号为k(1<=k<=1)开始报数,数到m的人出列,它的下一位又开始报数,数到m的人再次出列,直到所有人出列,由此产生一个新的编号。
- 创建一个环形链表,即修改头尾接的的next域,让其首尾相接
- 创建两个引用变量(指针)helper 和 first,first指向第一个节点,helper指向前一个节点
- 报数时两指针同时移动m-1次
- 将 first 指向的节点移出
待补充中
栈 Stack
栈是一种线性的数据结构,任意打开一个计算器,或使用一个高级的编程语言,它都能计算表达式,如(1+2*3+4/(5+6))结果的计算。计算机了解计算顺序和自动设置变量的个数,用到了栈的方法。不仅如此,栈的使用场景非常丰富。
栈遵循后进先出的概念,数据发生变化的一端称为栈顶(top),数据不变的一端称为栈底(bottom)。数据的进入称为进栈(入栈、压栈;push),数据的取出称为出栈(弹栈;pop)
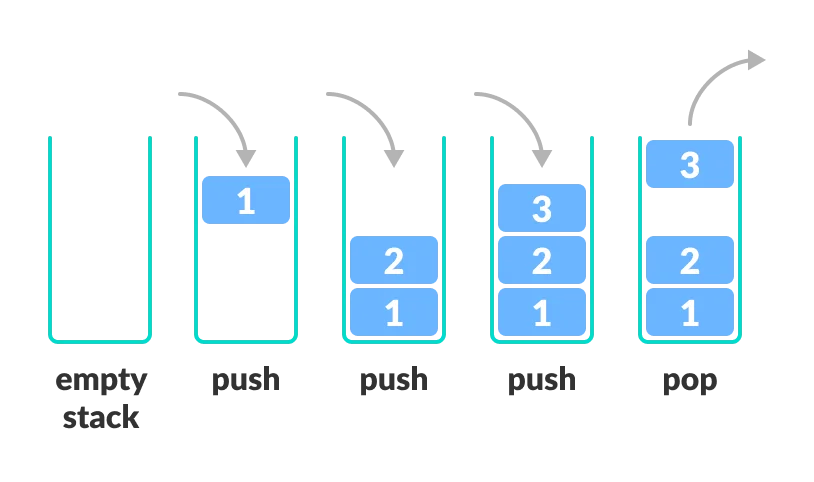
栈的实现
使用一 int 数组来模拟栈,数组中为 0 的元素记录为空,需要实现判断栈的状态(满/空)入栈、出栈、查看栈顶元素、显示所有元素功能。
栈的初始化
- 定义一个整形数组 simstuck
- 定义 top = -1, top 和数组的 index 对应
- 定义一个 size 变量,和一个构造器用于栈的初始化
栈的状态判断 isFull/isEmpty
- 当 top = -1 时栈为空
- 当 top = size – 1 时栈为满
入栈 push
- 判断栈是否已满
- top+1并将数据写入栈
出栈 pop
- 判断栈是否为空
- 使用一个临时变量存储栈顶值
- top-1并返回数据
代码
public class stackDemo {
public static void main(String[] args) {
stack stack = new stack(5);
stack.push(5);
stack.push(2);
stack.push(3);
stack.show();
System.out.println("peek:" + stack.peek());
System.out.println("pop:" + stack.pop());
System.out.println("peek:" + stack.peek());
stack.show();
System.out.println("pop:" + stack.pop());
System.out.println("peek:" + stack.peek());
System.out.println("pop:" + stack.pop());
System.out.println("peek:" + stack.peek());
}
}
/**
* stack
*/
class stack {
private int[] simStack;
private int top = -1;
private int size;
// constructor
public stack(int size) {
this.size = size;
simStack = new int[size];
}
public void push(int data) {
if (isFull()) {
return;
}
top++;
simStack[top] = data;
}
public int pop() {
if (isEmpty()) {
return -1;
}
int data = simStack[top];
simStack[top] = 0;
top--;
return data;
}
public int peek() {
if (isEmpty()) {
return -1;
} else {
return simStack[top];
}
}
public void show() {
if (isEmpty()) {
return;
}else {
for (int i = 0; i < simStack.length; i++) {
System.out.print(simStack[i]+";");
}
System.out.println();
}
}
private boolean isEmpty() {
if (top == -1) {
System.out.println("stack is empty");
return true;
} else {
return false;
}
}
private boolean isFull() {
if (top == size-1) {
System.out.println("stack is full");
return true;
} else {
return false;
}
}
}输出与思考
5;2;3;0;0;
peek:3
pop:3
peek:2
5;2;0;0;0;
pop:2
peek:5
pop:5
stack is empty
peek:-1使用链表来模拟栈:
public class linkedListStack {
public static void main(String[] args) {
stackNode stackNode01 = new stackNode(1);
stackNode stackNode02 = new stackNode(2);
stackNode stackNode03 = new stackNode(3);
stackNode stackNode04 = new stackNode(4);
stack simstack = new stack(3);
simstack.peek();
simstack.pop();
simstack.push(stackNode01);
simstack.push(stackNode02);
simstack.peek();
simstack.push(stackNode03);
simstack.push(stackNode04);
simstack.show();
simstack.pop();
simstack.show();
}
}
/**
* stack
*/
class stack {
private stackNode head;
private int size;
private int nowSize = 0;
// constructor
public stack(int size) {
head = null;
this.size = size;
}
// push() same as insertAtStart()
public void push(stackNode pushNode) {
if (head == null) {
head = pushNode;
} else if (nowSize == size) {
System.out.println("stack is full");
return;
} else {
pushNode.setNext(head);
head = pushNode;
}
nowSize++;
}
// pop() same as deleteAtStart()
public stackNode pop() {
if (head == null) {
System.out.println("stack is empty");
return null;
}
stackNode tempNode = head;
head = head.getNext();
nowSize--;
System.out.println("pop:" + tempNode.getData());
return tempNode;
}
// peek() same as getFirst()
public stackNode peek() {
if (head == null) {
System.out.println("stack is empty");
return null;
}
System.out.println("peek:" + head.getData());
return head;
}
// show() same as showList()
public void show() {
stackNode temp = head;
while (temp != null) {
System.out.print(temp.getData()+";");
temp = temp.getNext();
}
System.out.println();
}
}
/**
* stackNode
*/
class stackNode {
private int data;
private stackNode next;
// constructor
public stackNode(int data) {
this.data = data;
this.next = null;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public stackNode getNext() {
return next;
}
public void setNext(stackNode next) {
this.next = next;
}
}输出结果
stack is empty
stack is empty
peek:2
stack is full
3;2;1;
pop:3
2;1;可以看到使用链表同样可以模拟栈。
栈计算器 Stack Based Calculator
通过上述内容,了解了栈的实现方式和一些基本内容,现在开始编写一个计算器,需要实现以下功能:
- 表达式正确扫描
- 符号优先级判断
- 完成计算并输出结果
此次使用的栈由编程语言提供,不再模拟。
前、中、后缀表达式
中缀表达式
前、中、后表示的是运算符所在的位置,对于人常用的计算式如 1+2 是一个典型的中缀表达式,即运算符在两个数字中间。
中缀表达式对于人来说计算是最方便的,先算小括号里的式子,然后先乘除后加减。
但是对于计算机来说需要判断运算的优先级,这类简单的中缀表达式还可以勉强利用两个栈和优先级判断进行结果计算。如果计算式中包含多个小括号,多种运算符,那么对于计算机来说,处理起来是非常困难的。
前、后缀表达式 PN and RPN
波兰记法是波兰数学家扬·武卡谢维奇1920年代引入的,用于简化命题逻辑,即把符号写在数字之前将上式转换为 +12 ,这种表达式也被称为波兰表达式(Polish notation,或波兰记法)。
既然运算符能写到前面,那么也一定能写到后面,于是就有了 12+ 这种表达式。后缀表达式也叫做逆波兰表达式 Reverse Polish notation (RPN)。
在将中缀表达式转化为这类表达式的时候通过一个算法,可以去除表达式中的括号。计算机可以直接进行运算。
转换方法
以中缀表达式 a + b * c – (d + e)转后缀为例:
简易人工方法
- 按照运算符的优先级加括号(就是加一些没有影响的括号)该表达式变为 ((a + (b * c)) – (d + e))
- 将符号移到最后, ((a (b c)*) + (d e)+) –
- 把括号去掉,a b c * + d e + –
调度场算法 Shunting Yard Algorithm
维基百科
调度场算法(Shunting Yard Algorithm)是一个用于将中缀表达式转换为后缀表达式的经典算法
- 从左到右开始扫描中缀表达式
- 遇到数字输出
- 遇到运算符:
a. 优先级大于栈顶操作符,入栈
b. 优先级小于等于栈顶操作符,将栈内元素输出,将扫描到的运算符入栈 - 遇到 ( 将元素入栈,并将其优先级算为最低
- 遇到 ) 出栈、输出,( 只出栈,不输出
- 表达式扫描完毕,输出栈内的所有元素
对于表达式 a + b * c – (d + e)
- 遇到 a ,是个数字,输出或存在某个缓存(buffer)队列中等待输出,下略
输出:a
栈内:空 - 遇到 + ,是运算符,使用符号栈是空的,无输出,接着符号入栈
输出:a
栈内:+ - 遇到 b ,是个数字,输出
输出:ab
栈内:+ - 遇到* ,是运算符,优先级比栈内的 + 高,入栈
输出:ab
栈内:+* - 遇到c ,是个数字,输出
输出:abc
栈内:+* - 遇到- ,是运算符,优先级比栈内的*低,输出栈内符号,直到发现优先级更低的符号,入栈
输出:abc*+
栈内:- - 遇到( ,入栈
输出:abc*+
栈内:-( - 遇到d ,是个数字,输出
输出:abc*+d
栈内:-( - 遇到+ ,是运算符,栈顶是 (
输出:abc*+d
栈内:-(+ - 遇到e ,是个数字,输出
输出:abc*+de
栈内: -(+ - 遇到) ,输出,直到遇见 “(“,”(“只出栈不输出
输出:abc*+de+
栈内:- - 没有元素了,弹出栈内元素
输出:abc*+de+-
栈内:空
代码
RPN 计算
后缀表达式的运算先后顺序已经确定,计算机进行计算相对容易。对于后缀表达式,只需要定义一个栈,就可以进行运算了。以上式 abc*+de+- 为例:
- 逐个扫描后缀表达式的元素
- 遇到数字,入栈
- 遇到运算符,弹出栈中的两个数字,并计算
栈中的变化如下所示,由于示例表达式是代数式,原先的后缀表达式转化回了中缀表达式但实际结果已经计算出来了,可将任意数字带入 abcde 中进行计算。
- a
- a,b
- a,b,c
- a,b*c
- a+b*c
- a+b*c,d
- a+b*c,d,e
- a+b*c,d+e
- (a+b*c)-(d+e)
代码部分完善中…
递归 Recursion
算法思维系列/递归详解.md
递归的基本思想是某个函数直接或者间接地调用自身,这样就把原问题的求解转换为许多性质相同但是规模更小的子问题。我们只需要关注如何把原问题划分成符合条件的子问题,而不需要去研究这个子问题是如何被解决的。递归和枚举的区别在于:枚举是横向地把问题划分,然后依次求解子问题,而递归是把问题逐级分解,是纵向的拆分。
递归有助于分析、解决问题,例如将一个数组不断一分为二进行(归并排序)排序,使用递归代码会变得简洁明了,递归代码必须要有结束条件,否则就会进入死循环。
迷宫问题
使用一二维数组表示迷宫,二维数组中:
- 0:未探索区域
- 1:墙
- 2:走过了,可以走通
- 3:走过了,走不通
初始化一个简单的迷宫
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1需要从左上角的 0 走到右下角的 0 的位置,使用“下–>右–>上–>左”的顺序进行判断。对于二维数组中一个元素“[i][j]”每走一步对“[i+1][j]–>[i][j+1]–>[i-1][j]–>[i][j-1]”如果这些地方都走不通则标记3。
代码
public class maze {
public static void main(String[] args) {
// make a map
/*
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
* */
int[][] map = new int[8][7];
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
System.out.println();
setWay(map, 1, 1);
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
//i,j the start point
//6,5 the check point
//i,j == 0 not been this point
//i.j == 1 wall
//i,j == 2 a way
//i,j == 3 unable to go next point
//use down-right-up-left to find way
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {
return true;
} else {
if (map[i][j] == 0) {
map[i][j] = 2;
if (setWay(map, i + 1, j)) {
return true;//down
} else if (setWay(map, i, j + 1)) {
return true;//right
} else if (setWay(map, i - 1, j)) {
return true;//up
} else if (setWay(map, i, j - 1)) {
return true;//left
} else {
map[i][j] = 3; //all direction unable to go
return false;
}
} else {
return false;
}
}
}
}八皇后问题
在国际象棋棋盘上,放置8个皇后,每个皇后不能互相攻击。皇后的攻击范围以自己所在位置画横线、竖先、两个斜线,这些位置上不能有其他皇后。
使用一个一位数组可表示一种解,数组中的每个元素表示每个皇后在这一行的第几个位置。因为游戏规则,递归时第二个皇后不可能放在同一行,所以只需要判断是否在同一列
代码
public class Queen {
//define a max = numbers of queen
int max = 8;
static int count = 0;
static int judgeCount = 0;
//define a array store a result
int[] array = new int[max];
public static void main(String[] args) {
Queen queen = new Queen();
queen.check(0);
System.out.printf("Count:%d\nJudge:%d", count, judgeCount); //Count:92 Judge:15720
}
//print
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]);
}
System.out.println();
}
//judge
private boolean judge(int n) {
judgeCount++;
for (int i = 0; i < n; i++) {
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) { //The same column or the same slope
return false;
}
}
return true;
}
private void check(int n) {
if (n == max) {
print();
return;
}
for (int i = 0; i < max; i++) {
array[n] = i;
if (judge(n)) {
check(n + 1);
}
}
}
}